Comment calculer le rapport de grandissement en macrophotographie

Après un premier article consacré au matériel utilisé en macrophotographie, nous nous intéressons de plus près au rapport de grandissement. Comment le calcule-t-on, mais surtout, quels enseignements pouvons-nous tirer de ces formules a priori si barbares… et pourtant si concrètes !

Ce dossier macro est écrit par Jacques Croizer, déjà à l’origine de plusieurs tutoriels sur Nikon Passion, et auteur d’un guide qui simplifie la technique photo au profit du plaisir de photographier :

Tous photographes, 58 leçons pour réussir vos photos

Vous pouvez télécharger ce dossier macro au format PDF, cliquez sur le lien en fin d’article.

Le rapport de grandissement

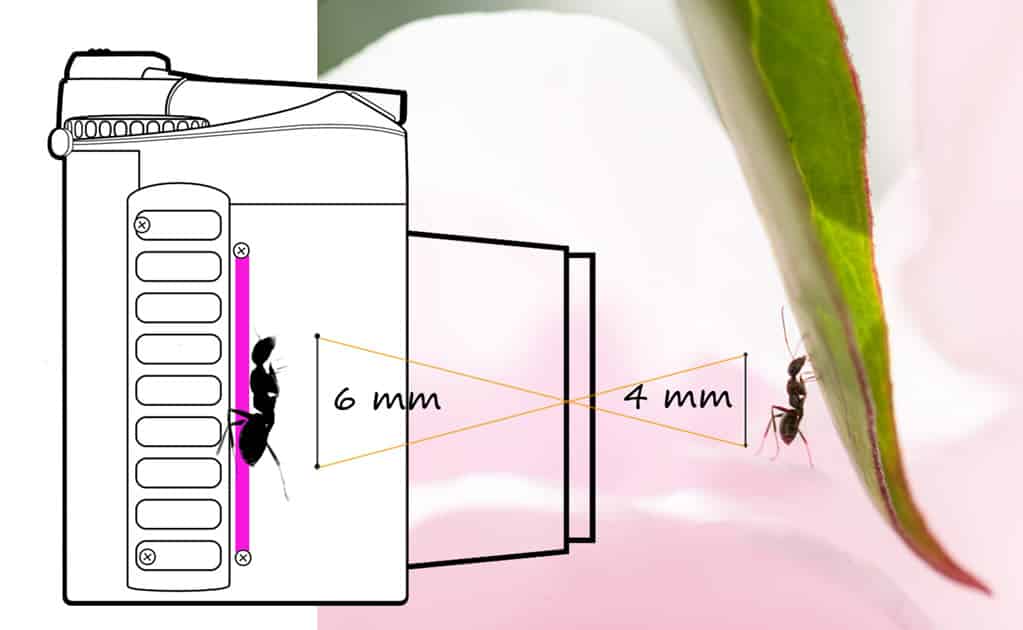
Rappelons que le rapport de grandissement caractérise l’effet loupe de l’objectif : c’est le rapport entre la taille réelle du sujet et celle de son image sur le capteur (voir le premier article de ce dossier).

Grandissement (C) J. Croizer

Dans cet exemple, la fourmi mesure 4 mm. Son image occupe 6 mm sur la hauteur du capteur. Le rapport de grandissement est donc égal à 6/4 = 1,5.  Remarquez que le rapport de grandissement ne dépend pas de la taille du capteur !

Rapport de grandissement de l’objectif standard

On appelle ici objectif standard n’importe quel objectif non macro. Que ce soit un grand angle ou un téléobjectif, son grandissement est nul lorsque la mise au point est faite à l’infini.

Sur la photo ci-dessous, le personnage occupe un cinquième de la hauteur du capteur plein format, soit 4,8 mm. Il mesure en réalité 1,70 m.

Nous sommes loin d’une mise au point à l’infini, mais le grandissement n’est pourtant déjà plus que 4,8/1700 = 0,0028.  Imaginez ce même calcul rapporté à la hauteur des montagnes à l’horizon…

Le photographe (f/10 à 1/8000 s – 50 mm) photo (C) J. Croizer

Lorsque le sujet est plus proche, le grandissement augmente. A la mise au point minimale, celui d’un objectif standard reste cependant encore très loin des attentes de la macro :

• il n’est par exemple que de 0,15 pour le Nikon AF-S NIKKOR 50 mm f/1.8G dont la mise au point minimale se situe à 45 cm,
• il monte à 0,24 pour le Nikon AF-S NIKKOR 300 mm f/4E PF ED VR avec une mise au point minimale à 1,4 mètre.

La bague allonge

La bague allonge est un moyen pratique pour vous initier à la macrophotographie sans investir dans un objectif macro. Elle permet d’éloigner l’objectif du boitier, et donc d’augmenter l’espace entre la lentille arrière et le capteur. On imagine bien sur la figure précédente que plus cette distance augmentera et plus l’image de la fourmi sera grande.

Afin de pouvoir faire varier le grandissement, on utilise généralement plusieurs bagues allonges, comme sur le jeu standard représenté ci-dessous. Il permet de décaler l’objectif du boitier de 12 mm, 20 mm ou 36 mm … ou tout autre combinaison de ces valeurs lorsqu’on empile plusieurs bagues.

Jeu de trois bagues allonges

Calcul du grandissement avec des bagues allonges

La longueur de la bague allonge est aussi appelée son tirage. Il est noté par la lettre T. Il permet de calculer le grandissement G d’un objectif de focale F lorsque la mise au point est faite sur l’infini :

G = T / F

Avec :

• T : tirage de la bague (par ex. 20 mm)
• F : focale de l’objectif (par ex. 50 mm)
• G : grandissement pour une mise au point à l’infini.

Dans notre exemple, le grandissement est égal à 20 / 50 soit 0,4 lorsque la mise au point est faite à l’infini. Nous sommes encore dans le domaine de la proxi photographie.

Que nous apprend cette formule ?

• Plus le tirage de la bague est important et plus le grandissement augmente : empilez plusieurs bagues pour atteindre des forts rapports de grandissement.
• Plus la focale diminue et plus le grandissement augmente : il est plus facile d’obtenir de forts grandissements avec une courte focale.
• Pour entrer dans le domaine de la macrophotographie (G = 1) lorsque la mise au point est faite sur l’infini, le tirage de la bague doit être au minimum égal à sa focale. Une bague de 36 mm utilisée avec un objectif de 30 mm permet d’obtenir un grandissement de 1,2 mais avec une focale de 50 mm, il faudra cumuler une bague de 36 mm et une bague de 20 mm pour dépasser le rapport 1.

Le même calcul de rapport de grandissement peut être fait pour le soufflet qui, d’un point de vue optique, se comporte comme une bague dont on peut faire varier le tirage.

Distance de mise au point avec des bagues allonges

La précédente formule est valable lorsque la mise au point est faite à l’infini. Soyez bien conscient que la distance réelle D qui vous sépare du sujet est bien moindre. Elle se calcule par la formule suivante :

D = F x (1+ 1/G)

Avec :

• D : distance réelle de mise au point
• F : focale de l’objectif (par ex. 50 mm)
• G : grandissement (par ex. 1)

Pour un grandissement de 1 avec un objectif de 50 mm, la distance réelle de mise au point est égale à 50 x (1+1/1) = 100 mm. Le sujet n’est plus qu’à 10 cm de l’objectif.

Cette formule est à nouveau riche d’enseignements :

Plus le grandissement obtenu est important, plus l’objectif est proche du sujet.

Plus la focale est courte, plus l’objectif est proche du sujet.

Pour photographier des sujets vivants sans les déranger, il est donc préférable d’utiliser des longues focales … mais comme nous l’avons vu précédemment, il est alors plus difficile d’obtenir de forts grandissements en ajoutant des bagues.

Quelques éclaircissements sur des notions d’optique

Utiliser la distance de mise au point à l’infini permet de calculer facilement le grandissement minimum qu’il est possible d’obtenir avec une bague allonge. Une fois sur le terrain, rien ne vous empêche de diminuer cette distance en vous rapprochant du sujet.

Revenons sur quelques notions pour bien comprendre ce qui va se passer :

• L’objectif a pour mission de reproduire sur le capteur l’image nette de la scène que vous voulez photographier.
• On appelle foyer principal image l’image d’un point situé à l’infini de la scène photographiée, dans l’axe de l’objectif. Si elle se forme en avant du capteur, cette image est floue.
• La distance entre cette image et le capteur est physiquement contrainte par celle qui sépare la baïonnette du capteur. On appelle cette dernière le tirage mécanique du boitier. Il est constant. Consultez la page Wikipedia (en anglais) pour connaitre celui de votre appareil.
• Dans le cas général, le tirage optique est la distance qui sépare le foyer principal image du sommet de la lentille la plus proche de la monture de l’objectif. Il varie avec la mise au point.
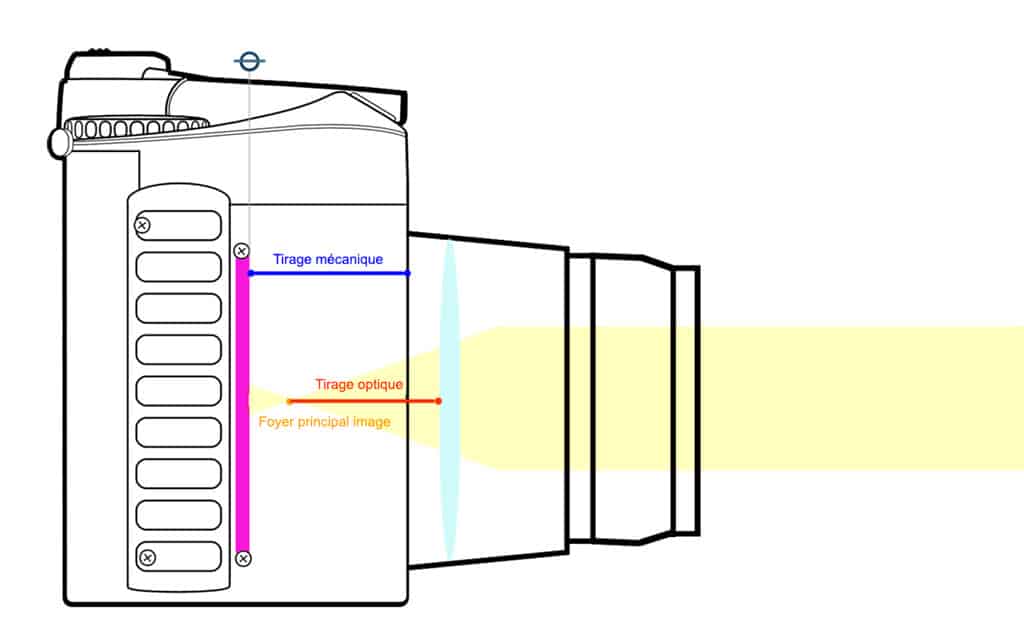
• C’est lorsqu’on fait la mise au point à l’infini que le tirage optique est le plus court. S’il est inférieur au tirage mécanique, il est impossible d’avoir une image nette. C’est le cas sur la figure ci-dessous, le plan de netteté ne peut pas être le même que le plan du capteur.

Principe de mise au point (C) J. Croizer

Dans un reflex, l’espace entre le capteur et la monture est encombré par le miroir. Sa disparition dans les appareils hybrides permet de réduire considérablement le tirage mécanique. Chez Nikon, il est passé de 46,5 mm pour la monture F à seulement 16 mm pour la monture Z.

L’emplacement du capteur est repéré par un symbole gravé sur le dessus du boîtier (généralement un cercle barré d’un trait).

Augmentation du grandissement avec des bagues allonges (objectif standard)

Laisser la mise au point sur l’infini n’est pas une fin en soi lorsqu’on fait de la macrophotographie. On cherche à accroitre le grandissement en se rapprochant du sujet.

Il faut alors ajuster la mise au point, c’est à dire reculer le centre optique de l’objectif, ce qui en modifie le tirage To. Pour un objectif standard, le tirage résultant se calcule par la formule suivante :

To = (Db x F) / (Db – F)

Avec :

• Db : distance sur la bague de mise au point (exemple 450 mm)
• F : focale de l’objectif (par ex. 50 mm)
• To : tirage de l’objectif

Cette formule vous apprend que lorsque la mise au point est faite à l’infini, le tirage de l’objectif est égal à sa focale. Il augmente lorsque la mise au point diminue.

Avec une focale de 50 mm et une mise au point à la MAP minimale (par ex. 45 cm, soit 450 mm) le tirage de l’objectif passe à 56,25 mm.

Lorsqu’on ajoute une bague de tirage T, le tirage total Tt est égal à T + T0. Le grandissement de l’ensemble s’exprime alors par la formule :

G = (Tt – F) / F

Avec :

• Tt : tirage total
• F : focale de l’objectif (par ex. 50 mm)
• G : grandissement résultant

Pour une MAP à l’infini, T0 est égal à F donc le grandissement dépend uniquement de l’épaisseur de la bague.

Avec une focale de 50 mm montée sur une bague de 20 mm et une mise au point à 45 cm (450 mm) on obtient :

• Tt = 20 + 56,25 = 76,25
• G = 0,525

On vérifie ?

Pour emplir la longueur d’un capteur plein format (36 mm) avec un grandissement de 0,525, le sujet photographié doit mesurer 36/0.525 = 68,6 mm.

Faisons le test avec un mètre scotché sur la porte du frigo. Il faut parvenir à un parfait parallélisme pour qu’il soit net sur toute sa longueur. Un trépied facilite l’opération qui reste cependant délicate :

50 mm + bague 20 mm – Mise au point à 45 cm

On mesure 67 mm sur le mètre, soit un grandissement de 0,537 proche de la valeur théorique. L’écart peut s’expliquer par l’incertitude sur le placement de l’appareil, liée à la profondeur de champ.

Ces formules n’ont pas pour seul but d’expliquer le grandissement. Vous pouvez les utiliser lorsque vous préparez une sortie pour optimiser le matériel à emporter en fonction du résultat attendu.

Distance réelle de mise au point avec des bagues allonges

Si on cumule une bague de 20 mm et une bague de 30 mm sur notre objectif de focale 50 mm, la précédente formule nous montre qu’on obtient un grandissement de 1,125 à la mise au point minimale.

Souvenez-vous qu’il était dans ce cas égal à 1 avec une mise au point à l’infini : le grandissement (donc le cadrage) varie finalement peu lorsqu’on tourne la bague de mise au point.

La distance réelle de mise au point D est bien évidemment inférieure à celle affichée sur la bague. La formule précédente reste valide :

D = F x (1+ 1/G)

Avec :

• D : distance réelle de mise au point
• F : focale de l’objectif (par ex. 50 mm)
• G : grandissement (par ex. 1,125)

Dans cet exemple, la bague de mise au point affiche une distance de 450 mm, mais la distance réelle de mise au point est à peine supérieure à 94 mm ! Elle était de 100 mm pour une mise au point faite à l’infini. Nous le savions déjà : la zone de travail est extrêmement réduite.

Calcul du grandissement avec un objectif inversé

Rappelons que la technique de l’objectif inversé consiste à utiliser une bague pour monter un objectif à l’envers sur le boîtier, voire même sur un premier objectif monté à l’endroit (montage tête-bêche).

La formule classique de calcul du grandissement pour une mise au point à l’infini reste valable :

G = (T – F) / F

Avec :

• T : tirage objectif + bague d’inversion
• F : focale de l’objectif (par ex. 50 mm)
• G : grandissement de l’objectif inversé

Ce calcul nécessite de connaitre précisément le tirage du nouvel ensemble, ce qui est rarement indiqué par les constructeurs. Si vous utilisez une bague d’inversion, consultez son manuel d’utilisation. Avec un peu de chance, vous y trouverez le rapport d’agrandissement pour les optiques les plus courantes, comme ici pour la bague Nikon BR2A (PDF).

En dernier recours, soyez pragmatique : utilisez la méthode du double décimètre comme nous l’avons fait précédemment.

Dans un premier temps, faites la mise au point à l’infini. Si le double décimètre est bien parallèle au bord de la photo et net sur toute sa longueur, il suffira de diviser la longueur du capteur par celle cadrée sur le double décimètre pour avoir une bonne approximation du grandissement minimal.

Et tant qu’à faire, n’hésitez pas à faire de même avec la mise au point faite au minimum pour connaitre le grandissement maximal !

Rapport de grandissement: cas de l’objectif macro

L’objectif macro a un grandissement qui lui est propre. Il est égal à 1 pour la mise au point la plus courte et diminue lorsque le sujet s’éloigne. Le grandissement résultant est alors parfois indiqué face au curseur de la bague de mise au point.

Lorsque l’objectif est monté sur une bague allonge, il serait logique de penser qu’il suffit d’ajouter le grandissement natif de l’équipement à celui procuré par la bague pour obtenir le grandissement total. Oui mais…

Les objectifs macro mettent en œuvre plusieurs groupes de lentilles qui se déplacent indépendamment l’un de l’autre pour faire la mise au point. La focale que l’on croyait fixe diminue d’autant plus que le sujet est rapproché !

Pour un grandissement de 1 à la distance minimale de mise au point Dm , la focale réelle Fm s’évalue simplement par la formule suivante :

Fm = Dm / 4

Avec :

• Fm : focale à la distance minimale de mise au point
• Dm : distance minimale de mise au point

Cette formule est démontrable pour une lentille simple. Le résultat n’est qu’une approximation pour un objectif dont la formule optique est bien évidemment plus complexe.

L’objectif Nikon AF-S VR Micro-Nikkor 105 mm f/2.8G IF-ED dont la distance minimale de mise au point est égale à 31 cm a dans ces conditions une focale résultante Fm de 77,5 mm ! C’est bien cette dernière valeur qui doit être prise en compte dans le calcul.

Par exemple, une bague de 36 mm intercalée entre et le boitier et ce 105 macro apportera un grandissement supplémentaire qu’il est possible d’évaluer par les formules suivantes :

Fm = Dm / 4 = 77,5

Avec :

• Fm : focale à la distance minimale de mise au point
• Dm : distance minimale de mise au point 310 mm

G = T / Fm = 0,46

Avec :

• T : tirage de la bague (par ex. 36 mm)
• Fm : focale de l’objectif (par ex. 77,5 mm)
• G : grandissement supplémentaire

Le grandissement total sera donc égal à 1 + 0,46 = 1,46 à la mise au point minimale. Pour ce réglage, un objet de 24,6 mm emplira la totalité de la longueur d’un capteur plein format.

On vérifie ?

105 mm + bague 36 mm – Mise au point à 31 cm

La longueur mesurée sur le mètre est de 23 mm. La procédure empirique peut partiellement expliquer l’écart constaté avec la valeur théorique, mais n’oublions surtout pas l’approximation faite en considérant que notre objectif n’est constitué que d’une seule lentille !

L’estimation du grandissement, avec ici une erreur de 7 %, reste cependant suffisante pour bien préparer sa sortie photo.

Rapport de grandissement : en conclusion

Connaitre précisément le rapport de grandissement d’un équipement n’est pas une fin en soi pour le photographe avant tout soucieux de l’esthétique de ses images. Les formules de calcul ne sont que le support à la réflexion. L’approche empirique dite du double décimètre reste le meilleur moyen de bien connaitre son matériel !

Dans le prochain article, nous parlerons lumière. En attendant, n’hésitez pas à partager votre retour d’expérience dans les commentaires.

La suite de ce dossier :

Comment faire de la macro photo

Comment gérer exposition et lumière en macro